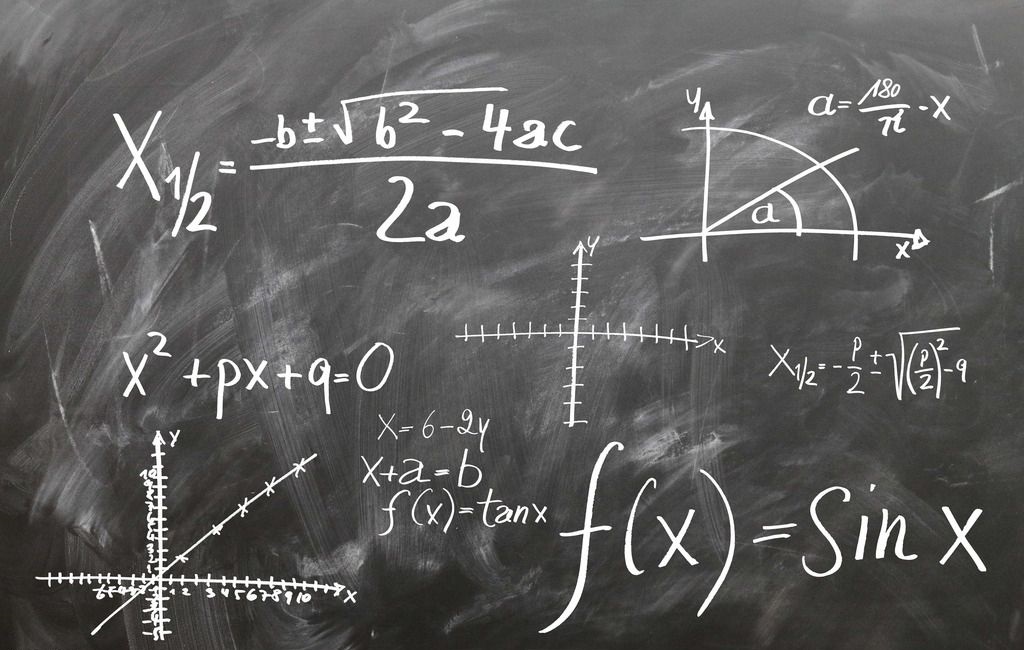已知$a,b,c,d \in \mathbf{R}$.求证 $\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+d^2}+\sqrt{d^2+a^2} \geq \sqrt{2}(a+b+c+d)$. 【分析】不等式左边是平面内某两点间的距离形式，由此联想构造距离来证明。 【证】取直角坐标系内四点：$A(a,b)$,$B(a+b,b+c)$,$C(a+b+c,b+c+d)$,$D(a+b+c+d,a+b+c+d)$. 平面内两点间所有连线中，直线段最短，所以 $\vert OA\ver…

$\displaystyle \sum^n_{k=1}\dfrac{2}{2k+1}\ln(n+1)<\ln(n+1)<\sum^n_{k=1}\dfrac{1}{\sqrt{k^2+k}}$ $\displaystyle \sum^n_{k=1}\dfrac{1}{\sqrt{2^k(2^k+1)}}>\ln \dfrac{2^{n+1}}{2^n+1}$ $\displaystyle \sum^n_{k=1}\dfrac{1}{k}>\ln(n+1)+\dfrac{1}{2}\dfrac…

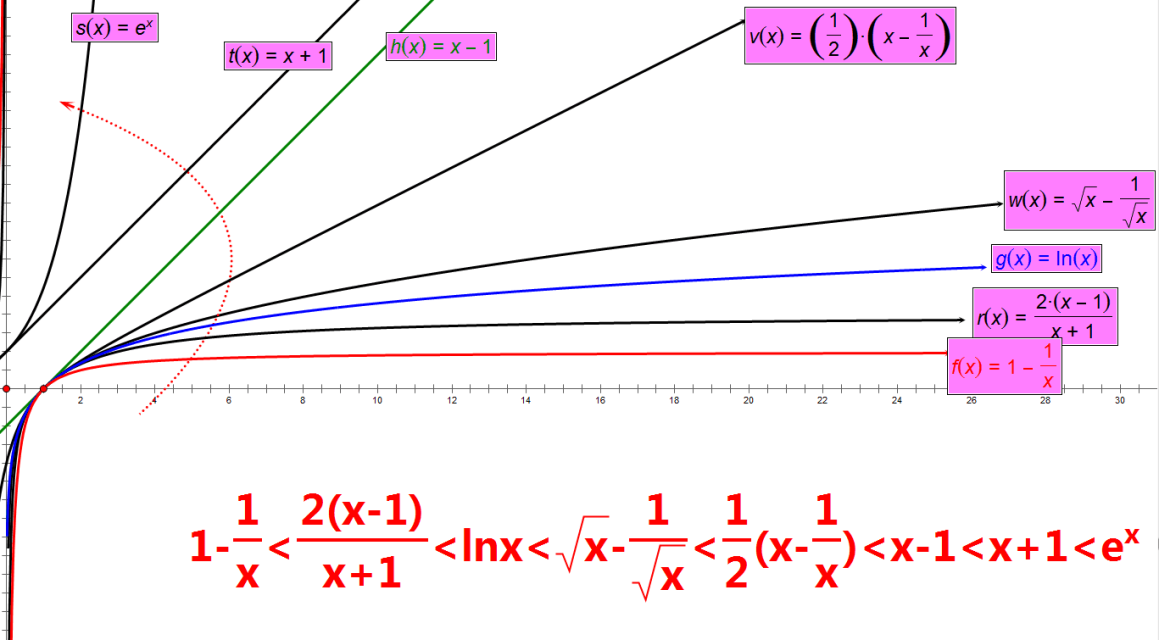
证明$e^x \geq 1+x$ 证明$e^{-x} \leq \dfrac{1}{1+x}$ , $x>-1$ 证明$e^{-x} \geq 1-x$ 证明$e^x \leq \dfrac{1}{1-x}$ , $x<1$ 证明$e^x \geq 1+x+\dfrac{1}{2}x^2$ , $x\geq 0$ 证明$e^{-x}\leq 1-x+\dfrac{1}{2}x^2$ , $x\geq 0$ 证明$\dfrac{x}{x+1}<\dfrac{2x}{x+2}<\ln(1+x)&…

　　相传，有一堆数学中的知识引发了以下名言：初中老师说，上了高中会学到的啦！高中老师说，初中不是学过了吗？ 　　而这样的问题还有许多，于是佛山一中的数学老师们为了祖国的花朵可以更快更好更强地茁壮成为祖国的栋梁，无偿抽出大量休息时间与精力，编写并年年修订《佛山一中初高中数学衔接》一书。 　　而十字相乘法便是其中的一个经典问题。有部分同学同学了解其原理，但未经大量练习来巩固；有部分同学只会二次项系数为1的，不为1的就不会；有部分同学甚至完全没有学过。而高考题中，几乎每种题型都涉及到一元二次方程的解决，而且是要求快速解决…

题目锐角 $\triangle ABC$ 中，已知 $a=\sqrt{3}$，$A=\dfrac{\pi}{3}$，则 $b^2+c^2+bc$ 的取值范围是 (A) $(3,9]$　　(B) $(5,9]$ (C) $(7,9]$　　(D) $(5,7]$   解法一由余弦定理，$a^2=b^2+c^2-2bc\cos A$，即 $3=b^2+c^2-bc$，得$b^2+c^2=bc+3$ 由正弦定理，$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin…